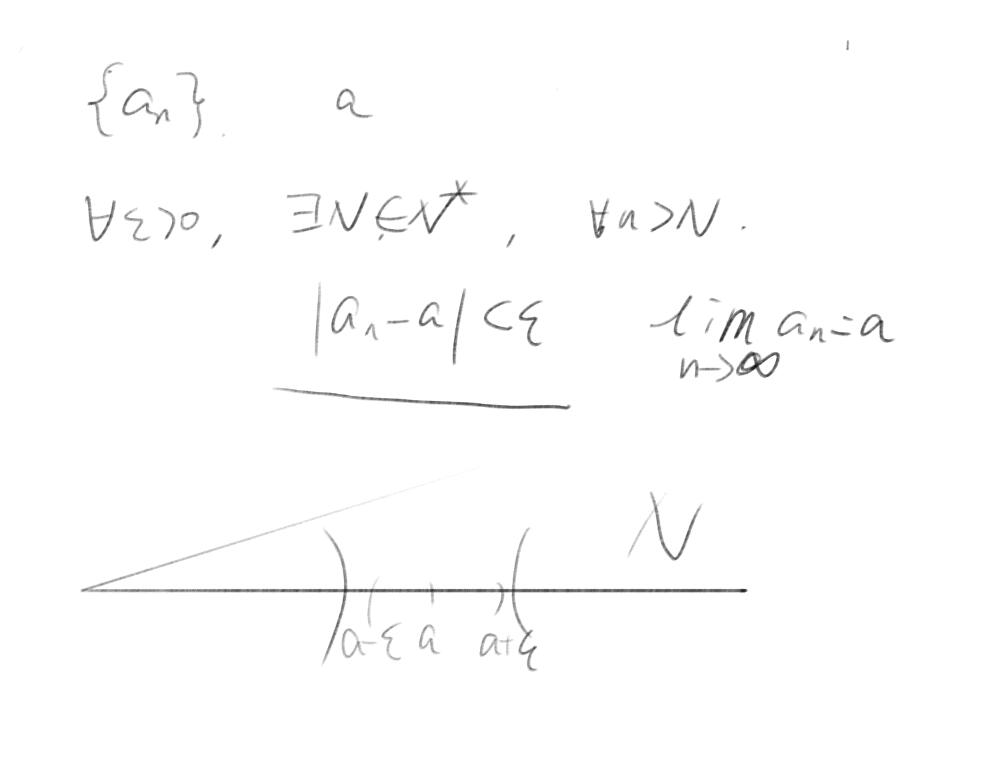
事先给定极限值a的ε邻域,找到一个N只要所有在N之后的n的值,也就是数列的项都落到ε邻域之内,那么就说这个数列是有极限的,极限值就是a,
邻域之外一定有有限个数列的项,就是事先给定的N个项,凡是掉落在ε邻域之内的项,误差都是可以接受的,也就是我们事先所说的任意小,当然不能是无穷小了,这个ε是和N有关系的,一般来讲,N越大ε越小,当然也不绝对。如果说一个数列有极限的情况下,在足够大的项后面一定是无限接近一个值,越靠后越接近,所以说邻域也就越来越小了,这只是一般情况下。
证明极限存在
当我们用极限定义来证明极限存在的时候,只需要证明出N的存在性就可以。也就是说只要有这么个N能使后面的无穷多项都落在ε邻域之内即可。不用找到最小的N,一般来讲怎么方便怎么来。
收敛数列的重要性质
1、数列的极限唯一
2、收敛数列一定有界
3、收敛数列的每一个子列都收敛同一个极限
网站内容来自网络,如有侵权请联系我们,立即删除!
Copyright © 驰雷百科 琼ICP备2024039176号-17